Mathematica 集合的表示与子集判断
来源:网络收集 点击: 时间:2024-08-26【导读】:
介绍Mathematica中集合的表示,子集的表示和判断,Mathematica中的Region的简单介绍。工具/原料moreMathematica方法/步骤1/8分步阅读 2/8
2/8
 3/8
3/8 4/8
4/8 5/8
5/8 6/8
6/8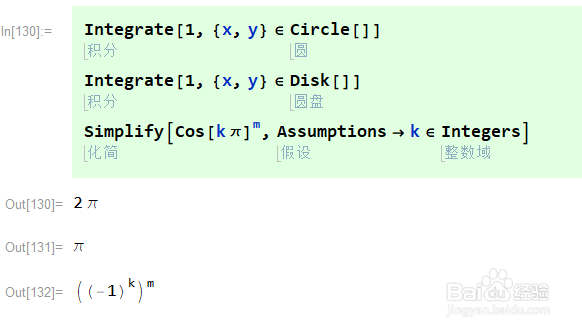 7/8
7/8 8/8
8/8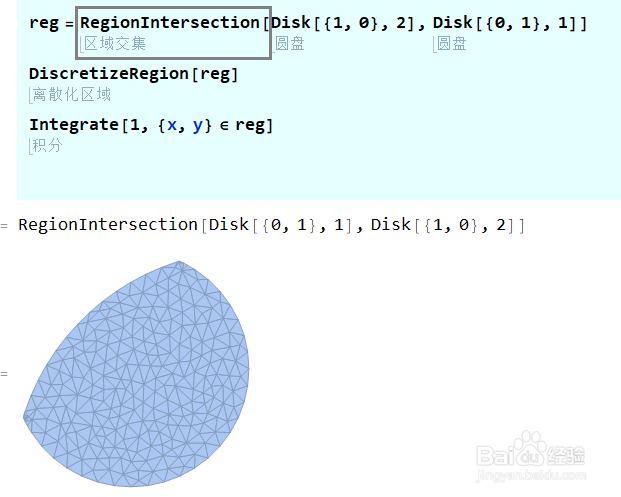
 注意事项
注意事项
MMA中,使用列表表示集合。集合有关的判断和运算也都基于列表。
列表中的重复元素,在集合有关运算时会被无视。
 2/8
2/8使用Subset以表示A是B的子集的意思。如图所示。
而使用SubsetQ则是判断B是不是A的子集。
两个集合相等的判断方法是,互相是子集。

 3/8
3/8集合中,可以有嵌套的列表。这些列表如何解释,和数学中集合套集合是一样的。对于整个集合来说,它们只是集合的元素。但是如果取出这个元素,也能参与别的集合运算。
 4/8
4/8如图,进行了几个子集判定,都为false。可见{1,2}是个元素。
和两个元素1,2不是一回事。
 5/8
5/8要想判断某个元素是否属于集合,可以使用MemberQ,判断a是否是A的元素。
Element仅仅表示数学符号。
 6/8
6/8在Mathematica中,还有一类,还有区域,和数域。区域是一些几何区域,如圆圈,圆形,球体等。可以参与计算。
数域有整数域,实数域,复数域。
 7/8
7/8如果我们直接对区域使用集合的函数和运算,不会得到想要的结果。
这些函数会按照列表处理。
 8/8
8/8处理区域,应该使用Region有关的函数。如图是求出两个平面区域的交集。
还可以在这个区域上做计算。不过这个计算结果十分复杂。

 注意事项
注意事项注意,Subset和SubsetQ的两个参数含义是反过来的。MemberQ和Element也是反的。
MATHEMATICA集合域子集版权声明:
1、本文系转载,版权归原作者所有,旨在传递信息,不代表看本站的观点和立场。
2、本站仅提供信息发布平台,不承担相关法律责任。
3、若侵犯您的版权或隐私,请联系本站管理员删除。
4、文章链接:http://www.ff371.cn/art_1157924.html
上一篇:怎么更换汽车之家app绑定的手机号
下一篇:钉钉中在哪查看订单记录信息
 订阅
订阅