本期分享主要讲解ANSYSWORKBENCH后处理中各种应力结果的详细说明。工具/原料more推荐自学视频教程：20天精通ANSYS教程获取更多学习教程可以查看我的个性签名！方法/步骤1/12分步阅读

在ANSYS WORKBENCH的结构分析后处理中，我们经常会关注应力。在选择一个对象并查看某种应力后，会在其细节视图中出现一个积分点结果的显示选项，说明要观察应力的哪种结果，如下图。

2/12

这里面有七种查看应力的方式。那么这些方式分别是什么含义呢？

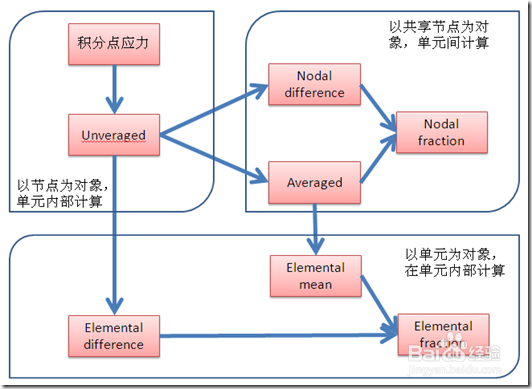
由于应力是我们做结构力学分析时最为关注的对象，因此弄清楚ANSYS所给的应力究竟是什么意思也就变得非常重要。这七种应力的含义及相互关系如下图。

3/12

从上图中可以看到，在计算出积分点的应力以后，其它应力都是在其基础上推算出来的。下面说明每一个选项的推算过程。

（1）unveraged---------没有平均化的应力。此时在单元内部，基于积分点的应力根据形函数推算该单元几个节点的应力。因为它是在积分点应力的基础上做的第一次运算，所以相对准确。此时如果一个节点周围毗邻几个单元，那么这几个单元在同一点处会有不同的应力值。

（2）areraged--------节点的平均化应力。在对所有单元进行计算，得到其节点的应力后，此时对于共享节点，对该点的几个应力进行平均，得到该点的应力。

（3）nodal difference---节点应力差的最大值。对于共享节点，还没有进行应力平均时，它有几个应力，对这几个应力排序，得到最大值，最小值；用最大值减去最小值，得到的值称为nodal difference.

(4) nodal fraction------对于一个共享节点，用（3）除以（2），得到一个比率，就是nodal fraction.

所以，（2）（3）（4）都是对于共享节点，在不同的单元间进行计算的。

（5）elmemntal difference-----在一个单元内部操作。找到单元内部节点应力的最大值，最小值，用最大值减去最小值，得到一个值，称为elemental difference.

(6) elemental mean---------在一个单元内部操作，在节点应力平均后，对于单元内所有的节点应力，再一次平均，得到单元内部的elemental mean.

(7)elemental fraction------在一个单元内部，用（5）除以（6），得到elemental fraction.

可见，（5）（6）（7）都是针对某个特定的单元所做的计算。

为了直观的说明上述计算过程，我们举一个例子。

例子如下，有3个四边形单元，一共8个节点。其中，

单元1由3,4,5,6四个节点构成

单元2由1,2,3,4四个节点构成

单元3由2,3,8,7四个节点构成

4/12

现在我们首先根据单元内部积分点的应力得到了如图所示的几个应力，即：

在单元1内部，基于积分点的应力值得到

节点3----应力是18MPa,

节点4----应力是12MPa,

节点5----应力是16MPa,

节点6----应力是14MPa,

在单元2内部，推出节点3-----应力是24MPa,节点4-----应力是12MPa,

在单元3内部，推出节点3-----应力是28MPa,

至于单元2,3内的其它节点，自然有应力，不过这里只想说明上述七项的计算方法，所以就不用赘述了。

下面说明上述七项的计算方法。

（1）unveraged-----没有平均化的应力。上面给出的节点应力均未平均化，都是unveraged.

对于（2）（3）（4），我们以节点3为例来说明。

（2）areraged = （18+24+28）/3 = 23.33 (MPa)，它是一个平均值。

（3）nodal difference：在18,24,28三个值中，最大是28，最小时18，因此nodal difference= 28-18 =10(MPa)。

(4) nodal fraction=10/23.33 = 0.43

对于（5）（6）（7）我们以单元1为例来说明。

（5）elmemntal difference：该单元内部节点应力最大值是18，最小是12，因此elmemntal difference=6Mpa.

(6) elemental mean = (14+16+12+23.33)/4 = 16.33(MPa).

(7) elemental fraction = 6/16.33=0.37.

由此可见，

（1）（3）（4）所表现的是一个节点周围单元在此处的应力梯度。

（5）（7）所表现的是一个单元内部的应力梯度。

（2）（6）则是均匀化的应力和单元解。

5/12

上面说明了各种应力结果的含义，这里再看一个实际的例子，并考察ANSYS WORKBENCH在后处理中的各种云图显示效果。

几何模型如下图

6/12

在左边和下边施加无摩擦支撑，右边施加水平向右的分布力系，载荷集度为1MPa.

划分网格后得到的有限元模型如下

7/12

现在考察X方向正应力的各种结果。

（1）未均匀化的节点应力解

【评】在每一个单元内部，先得到积分点的应力后，外推得到各个节点处的应力。观察尖角处可以看到，在节点的四周颜色并不一样，这意味着在同一个节点处会有几个应力出现。所以每个点的应力呈现为多值性。

这里的应力是最初计算出来的应力，相对比较准确。

8/12

均匀化后的节点应力解

【评】均匀化后，我们可以看到，每个节点处只有一个颜色，此时一个节点只有一个应力值。

9/12

节点的最大应力差

【评】该值总是正数，因为是用节点应力的最大值减去最小值得到的。我们可以发现，在尖角处，应力差很大，这意味着，从不同的单元在递推该节点的应力时，值相差很远。

显然，该图是很有用处的，它反映了应力梯度在哪个节点上最大，这正是应力集中发生的地方。

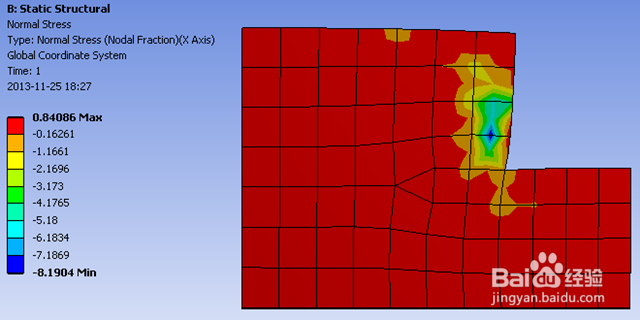
10/12

节点的应力分数

【评】我们可以看到，应力分数有正有负，这是因为它是由（3）/(2)后得到的。虽然（3）总是正数，但是（2）则有正有负。

该值是一种相对误差的概念，意味着当节点取得平均应力后，其误差是多大。该值的绝对值越大，则意味着平均化导致的误差越大。

11/12

单元内部节点的最大应力差

【评】它意味着单元内部的应力梯度。该值越大，意味着该单元自身内部应力变化很大，这也意味着该单元应该进一步细分才能得到更正确的结果。

（6）单元内部节点的平均应力

（7）单元内部节点的应力分数

【评】它同样是一个相对误差的概念。意味着单元取得平均值后的误差。该值的绝对值越大，同样意味着单元值平均化后导致的单元应力误差越大。

12/12

【总结】

结果(1)未均匀化的节点应力解是最正确的结果，它应该是进行结果考察的主要依据。

结果（3）和（5）所反映的分别是节点处，以及单元内的应力梯度。应力梯度大，意味着此点及此单元应该进一步细分网格，所以该云图是网格细分的依据。

结果（2）和（6）所反映的是节点，单元的平均应力。当我们想获得某一个节点或者单元的应力时，会选取此值。

结果（4）和（7）分别反映着当我们用平均值来代表该节点，单元的值时，其可靠度有多大。该值的绝对值越大，则意味着用平均值来代替该点或者单元值时，误差可能会比较大。它是我们选取平均值的一个判据。此值的绝对值越大，意味着我们选用此平均值作为该对象的值时，其可靠度越低。