介绍线性同余方程组的求解方法。使用Mathematica化简，计算等。工具/原料moreMathematica方法/步骤1/12分步阅读

首先，如果两个数，模a,b,c同余，那么它们模(a,b,c)同余。且模(a,b,c)同余可以表示所有解。

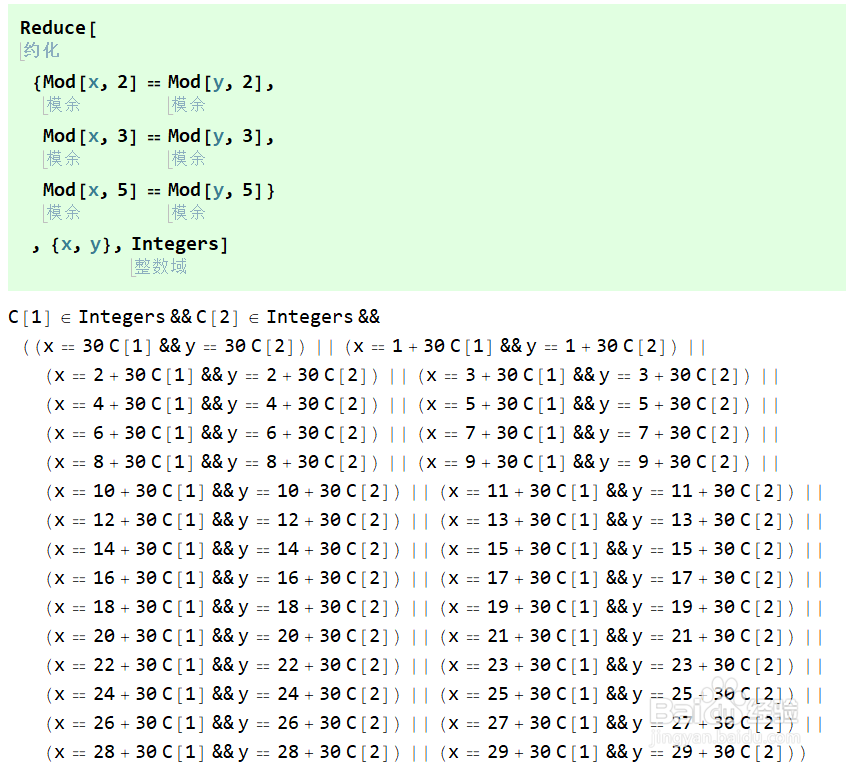
使用Reduce化简同余方程，指定域为Integers整数域。

2/12

为了使得结果简洁，我们设成x≡x+y(mod 2,3,5)，这样Reduce以后，使用Simplify化简，就只有一项。

可见，y是30的倍数。

3/12

此处还可以使用Solve求解。得到的是条件表达式。

Solve的结果使用/.替换，并带入C即可以得到数值结果。

4/12

下面，我们说只有一个变量的同余方程组，比如如图的方程组，各个模数是互素的。

使用Reduce直接得出结果为23(mod 105)

5/12

下面说分步求解过程：

首先使用LCM求得各个模数的最小公倍数，除以各个模数，得到M1,M2,M3。

最终的结果是M1,M2,M3的线性组合。

6/12

接下来，求解如图三个互相无关的线性同余方程。

就是依次把原来方程中的x换成a*M1+b*M2+c*M3，然后消去无关项，个个方程就独立了。得到如图3个方程。

分别求解出a,b,c。

7/12

这里，C带入任意数都可。带入0比较好算。得到a=1,b=3,c=2。

然后计算a*M1+b*M2+c*M3，得到128为原来线性同余方程组的一个解。

8/12

最后，对这个解模LCM，即三个模数的最小公倍数105，得到解的形式为

x≡23 (mod 105)

9/12

如图，演示了带入常数为C=1，最终模完仍然是23。故常数C无关紧要。

10/12

下面说模数不互素时的解决方法。

首先，如图方程组为例，使用Reduce也可以直接求解。

11/12

根据第一个方程，设x=6t+4，带入第二个，求出t。

12/12

然后根据t求出x。解x模LCM(m1,m2)同余。如图，LCM(m1,m2)=24，故解为x≡10(mod 24)

注意事项

之所以结果是M1,M2,M3的线性组合，因为对于第一个方程a1*x≡b1(mod m1)来说，M2和M3不论怎么组合都是0(mod m1)。这样只需要根据第一个方程求出M1的系数即可。第二个第三个方程同理。

MATHEMATICA线性同余方程组同余数论