本文介绍如何用MATLAB仿真产生FIR滤波器，并使用一个混合频率的信号通过FIR滤波器，观察其输出，以验证FIR滤波器性能。工具/原料moreMATLAB软件方法/步骤1/6分步阅读

实际应用背景：若信号为一个10Hz与一个30Hz的余弦信号相加，那么如何滤除30Hz的信号？

2/6

首先产生原始信号。采样率设置为100Hz，时宽2s。

MATLAB程序如下：

f1=10;%第一个点频信号分量频率

f2=30;%第二个点频信号分量频率

fs=100;%采样率

T=2;%时宽

B=20;%带宽

n=round(T*fs);%采样点个数

t=linspace(0,T,n);

y=cos(2*pi*f1*t)+cos(2*pi*f2*t);

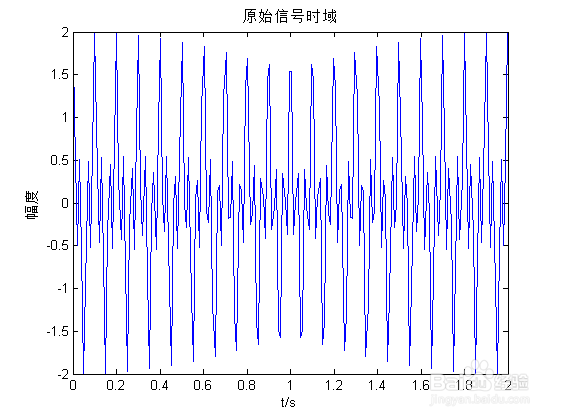
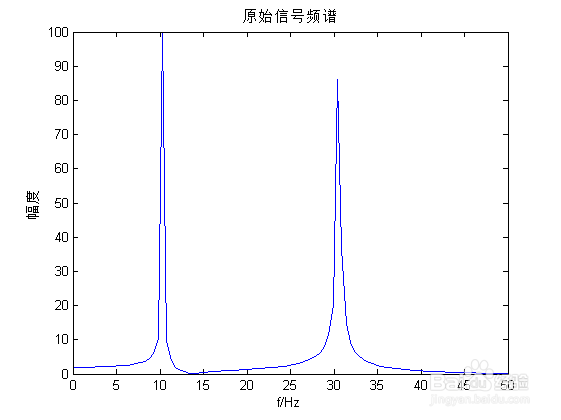
3/6

观察原始信号的时域波形和频谱，从频谱图中可以明显看出其10Hz与30Hz的分量。

MATLAB程序如下：

figure;

plot(t,y);

title(原始信号时域);

xlabel(t/s);

ylabel(幅度);

figure;

fft_y=fftshift(fft(y));

f=linspace(-fs/2,fs/2,n);

plot(f,abs(fft_y));

title(原始信号频谱);

xlabel(f/Hz);

ylabel(幅度);

axis();

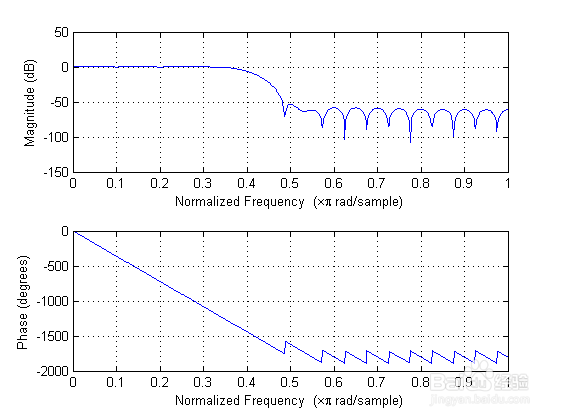
4/6

设计FIR滤波器：为滤除30Hz的分量，我们选用20Hz截止频率的低通滤波器，阶数为40阶（若要获得更陡峭的过渡带，阶数可以选择的更高）。MATLAB中用fir1函数实现滤波器冲击响应系数的计算。注意:模拟频率f=20Hz需要按f/(fs/2)的式子化为数字频率，作为fir1函数中的参数。

MATLAB程序如下：

b=fir1(40, B/(fs/2)); %滤波产生指定带宽的噪声信号

figure;

freqz(b);%画滤波器频响

5/6

信号通过FIR滤波器：采用filter函数。

MATLAB程序：

y_after_fir=filter(b,1,y); %信号通过滤波器

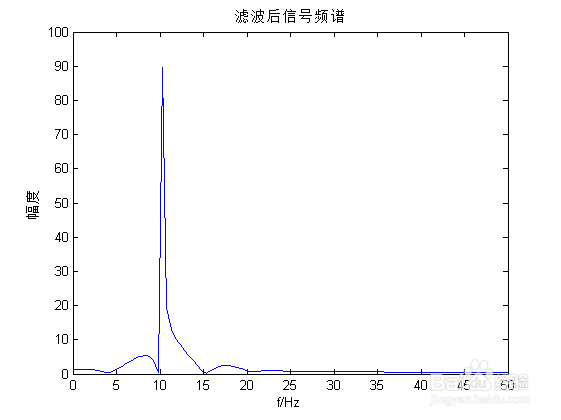
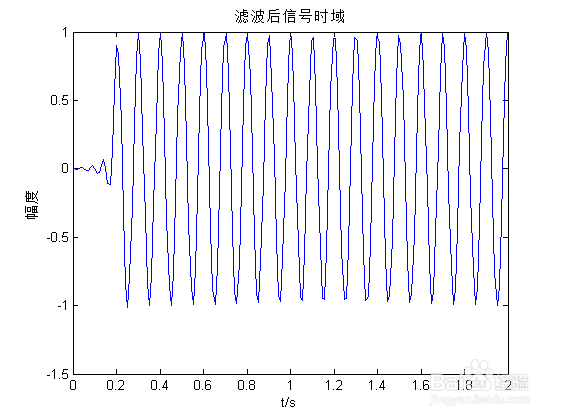
6/6

观察滤波后输出信号的时域与频谱：

从频谱中可以明显看出，30Hz的分量被滤除，留下了10Hz的分量。时域波形也可以看出这一点。同时需要注意，输出信号的前面一段是无效的。该段的长度为滤波器阶数的一半。

MATLAB程序：

figure;

plot(t,y_after_fir);

title(滤波后信号时域);

xlabel(t/s);

ylabel(幅度);

fft_y1=fftshift(fft(y_after_fir));

f=linspace(-fs/2,fs/2,n);

figure;

plot(f,abs(fft_y1));

title(滤波后信号频谱);

xlabel(f/Hz);

ylabel(幅度);

axis();

注意事项

在实际设计中，可以通过加窗函数的方法抑制频谱泄露

相比较于IIR滤波器，FIR可能所需阶数更高，但同时由于其非迭代结构，永远能够得到稳定的输出。

MATLABFIR数字低通滤波器频谱频率响应