对f(x)做周期为2π的奇拓展，将f(x)拓展为实数域上的奇函数，由狄利克雷定理可知f(x)可以拓展为傅里叶级数。

设f(x)=a_{0}+ Sigma(a_{n}cosnx)+Sigma(b_{n}sinnx)；（Sigma从1到无穷求和）

两边乘以cosnx，在(-π,π)上求定积分可得a_{n}=0；

等式两边在(-π,π)上求定积分可得a_{0}=0；

两边乘以sinnx，在(-π,π)上求定积分可得b_{n}=(-1)^{n+1}2/n；

最后一步的计算过程中（sinnx）^2在(0,π)上的定积分为π/2；

xsinnx在(0,π)上的定积分为}=(-1)^{n+1}π/n。

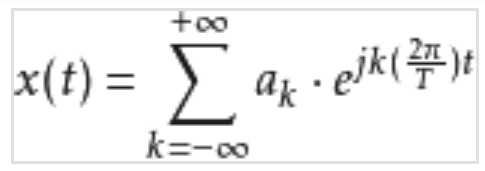
傅里叶级数来源：

法国数学家J.-B.-J.傅里叶在研究偏微分方程的边值问题时提出。从而极大地推动了偏微分方程理论的发展。在中国，程民德最早系统研究多元三角级数与多元傅里叶级数。

他首先证明多元三角级数球形和的唯一性定理，并揭示了多元傅里叶级数的里斯- 博赫纳球形平均的许多特性。傅里叶级数曾极大地推动了偏微分方程理论的发展。在数学物理以及工程中都具有重要的应用。