Mathematica 指数分布
来源:网络收集 点击: 时间:2024-05-21【导读】:
使用Mathematica计算指数分布,用指数分布计算寿命,指数分布的性质推导,以及指数分布的绘图。工具/原料moreMathematica方法/步骤1/7分步阅读 2/7
2/7 3/7
3/7
 4/7
4/7 5/7
5/7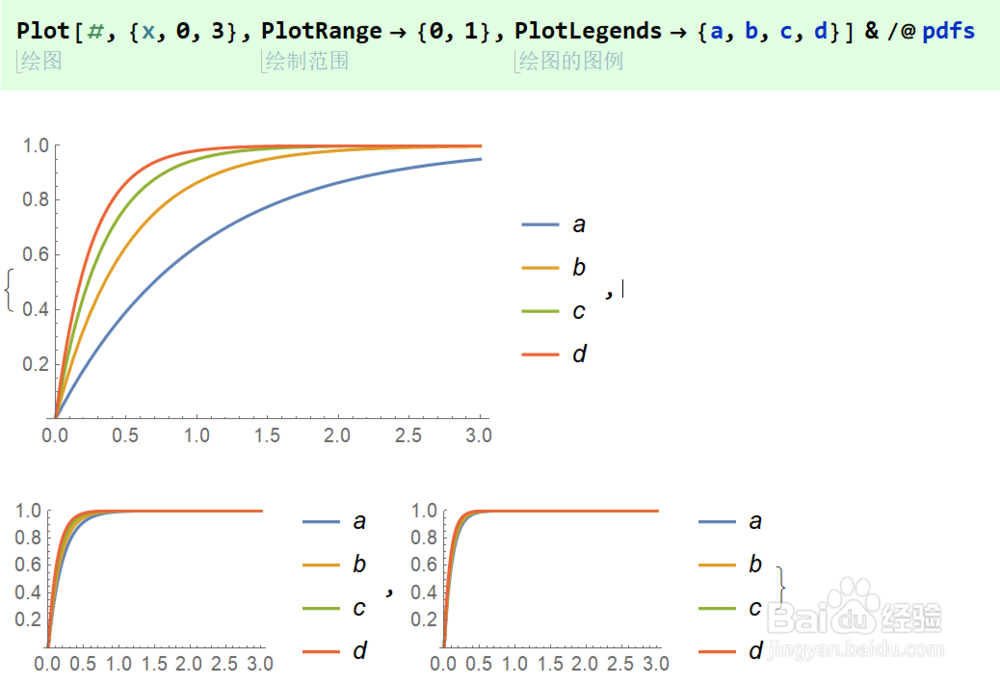 6/7
6/7 7/7
7/7 注意事项
注意事项
在Mathematica中,指数分布的符号是ExponentialDistribution,该分布只有一个参数。
 2/7
2/7指数分布是[0,+∞)上的分布。其概率密度函数为λe^(-λx),x0
其累计分布函数如图。
 3/7
3/7接下来,使用如图代码产生λ分别等于1,2,3,4时的概率密度函数如图所示。
然后使用Plot绘制图像,可以看到λ越大,原点处概率密度越高,概率密度下降越快。

 4/7
4/7接下来,我们使用Mathematica中的纯函数语法嵌套,产生λ从1~12的累计分布函数,并且4个一组。
 5/7
5/7使用Plot函数配合纯函数和映射,绘制三个图,分别是λ=1,2,3,4,λ=5,6,7,8,λ=9,10,11,12。
累计分布的初始时刻斜率为λ。
 6/7
6/7指数分布可用来表示零件寿命。
如果单位时间内原件故障损坏的难易程度用λ的大小表示,即假设原件每一瞬间发生故障的难易程度相同,则:
指数分布就是原件的寿命分布。
 7/7
7/7指数分布无记忆性。如果把随机变量看为时间,则不论从什么时候开始的条件分布,都和原分布相同。
 注意事项
注意事项注意无记忆性是从某一时刻以后的条件分布与原来相同,这对于故障率恒定的零件的寿命来说,是显然的。
MATHEMATICA指数分布概率密度版权声明:
1、本文系转载,版权归原作者所有,旨在传递信息,不代表看本站的观点和立场。
2、本站仅提供信息发布平台,不承担相关法律责任。
3、若侵犯您的版权或隐私,请联系本站管理员删除。
4、文章链接:http://www.ff371.cn/art_818938.html
上一篇:制作沙画要做什么准备工作
下一篇:最终幻想10键盘设置
 订阅
订阅