考研高数:无穷小怎么比较,基本定义有哪些?
来源:网络收集 点击: 时间:2024-02-22【导读】:
如果有两个都是无穷小的值,那么它们比较会有什么区别吗?下面这里给大家介绍下,无穷小比较的基本定义。下面介绍的α,β,都是无穷小,且无穷小α不为0.无穷小怎么比较,基本定义有哪些1/7分步阅读 2/7
2/7 3/7
3/7 4/7
4/7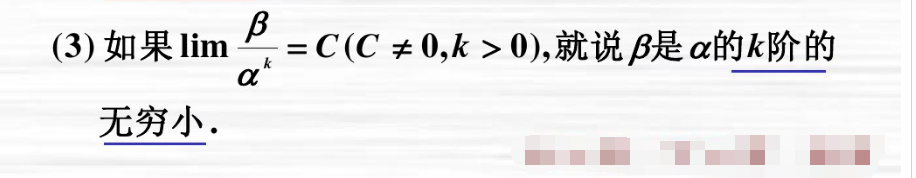 5/7
5/7 6/7
6/7 7/7
7/7
高阶无穷小,
如图
就是说α比β更快的趋向于无穷小,
例如(n+1)/n^2,
就是(n+1)是n^2的高阶无穷小
 2/7
2/7同阶无穷小
例如: 当x趋向于3时,(x^2-9)/(x-3)=6,
就是同届无穷小。
 3/7
3/7等价无穷小
这个最典型的例子就是
当x-0时,sin(x)/x = 1
所以这时候,sin(x)和x就是等价的无穷小。
 4/7
4/7k阶无穷小
定义如图,
示例参考
当x-0时(1-cos(x))/x^2 = 1/2,
所以,1-cos(x)是x的k阶无穷小。
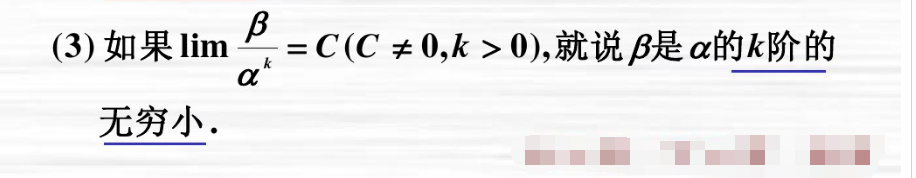 5/7
5/7和第一个想对应的,
如果结果是无穷大∞,
那么β是α的低阶无穷小,
β比α更快的趋向于无穷小
 6/7
6/7最后经常会使用到
等价无穷小,
一般表示为
β=α+o(α)
 7/7
7/7等价无穷小的替换法则
如图
等价无穷小可以这样替换的

版权声明:
1、本文系转载,版权归原作者所有,旨在传递信息,不代表看本站的观点和立场。
2、本站仅提供信息发布平台,不承担相关法律责任。
3、若侵犯您的版权或隐私,请联系本站管理员删除。
4、文章链接:http://www.ff371.cn/art_97205.html
上一篇:皮皮虾app怎么扫脸
下一篇:闲鱼在哪查看动态
 订阅
订阅