怎么判断函数是否可导
来源:网络收集 点击: 时间:2024-09-01【导读】:
函数的导数对于函数的分析非常有用的,简单来说,一阶导数求速度,二阶导数求加速度,等等。那么一个函数怎样才能判断是否可导呢?我在这里对一元函数,二元函数的可导性判断做了一个总结。工具/原料more一元函数二元函数求导公式一元函数可导性判断方法1/4分步阅读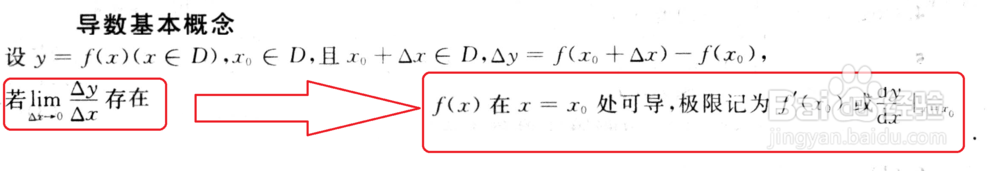 2/4
2/4 3/4
3/4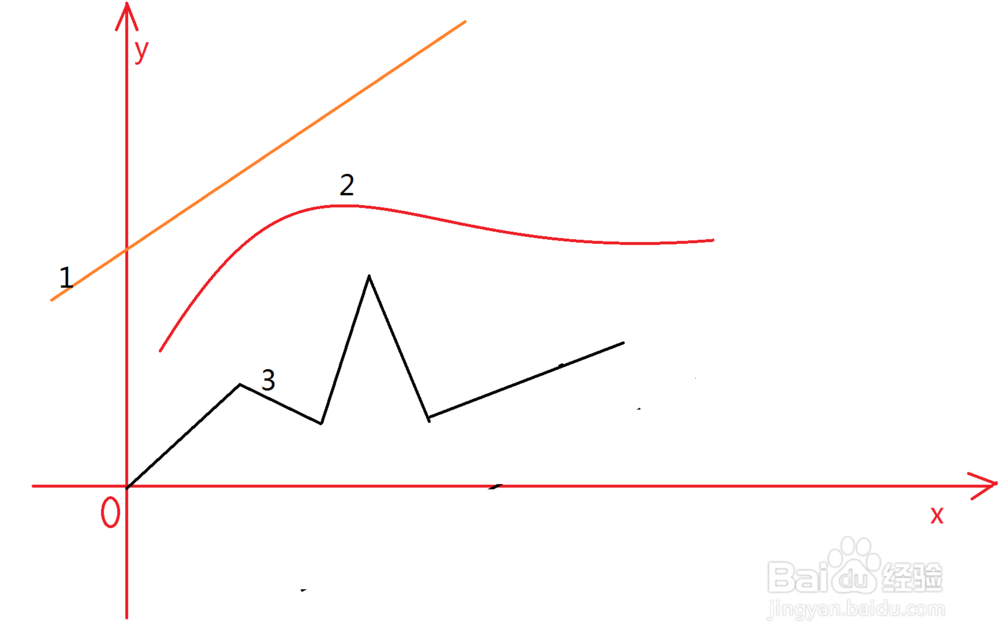 4/4
4/4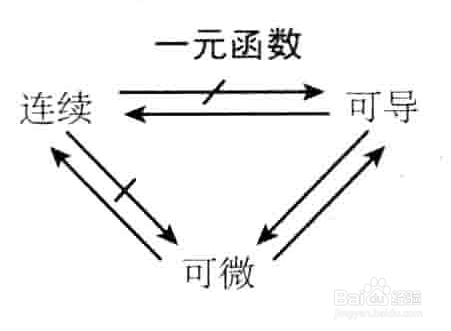 二元函数可导性判断方法1/3
二元函数可导性判断方法1/3 2/3
2/3 3/3
3/3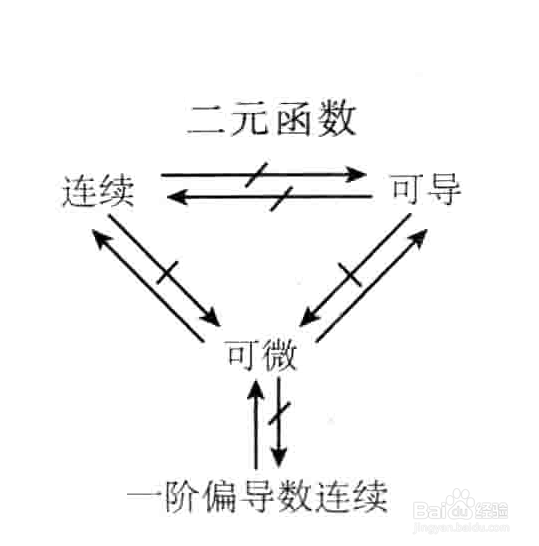 多元函数可导性判断方法1/1
多元函数可导性判断方法1/1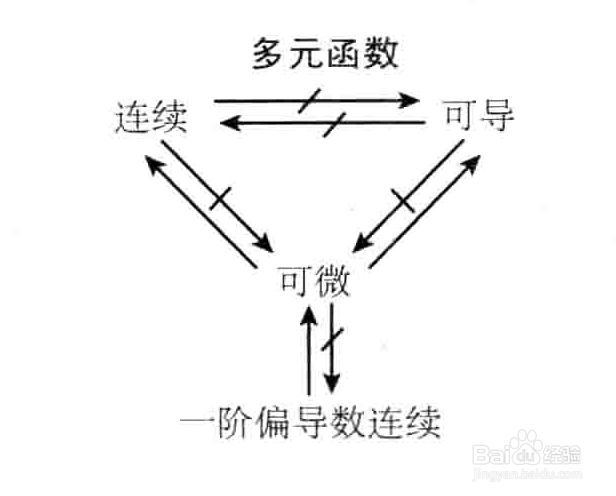 注意事项
注意事项
定义法判断一元函数是否可导。
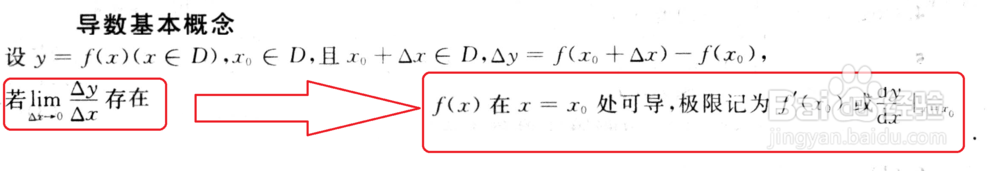 2/4
2/4常见的初等函数,或者初等函数之间的基本运算均可导。如图:
 3/4
3/4图形观察:函数图像是光滑曲线,这样的函数可导。记住“光滑”的含义:没有棱角或者尖角。线1,2可导,3不可导。
 4/4
4/4经验小结:如图。
 二元函数可导性判断方法1/3
二元函数可导性判断方法1/3定义法:可微是可导的充要条件。
 2/3
2/3图形观察:(x,y)形成的曲面是“光滑的”,“不硌手”,“不伤手”,则可导。
 3/3
3/3经验小结:如图。
 多元函数可导性判断方法1/1
多元函数可导性判断方法1/1多元函数可导性判断方法与二元函数可导性判断方法类似
 注意事项
注意事项一元函数可导性与多元函数可导性判断准则不一样
二元函数可导性判断可用于多元函数可导性的判断
一元函数求导二元函数求导可导性判断求导公式版权声明:
1、本文系转载,版权归原作者所有,旨在传递信息,不代表看本站的观点和立场。
2、本站仅提供信息发布平台,不承担相关法律责任。
3、若侵犯您的版权或隐私,请联系本站管理员删除。
4、文章链接:http://www.ff371.cn/art_1183068.html
上一篇:腾讯手机管家中怎么解除qq绑定
下一篇:香蕉燕麦纸杯蛋糕的做法
 订阅
订阅