订阅求可逆矩阵的方法
来源：网络收集 点击： 时间：2024-04-06【导读】：
矩阵对应的行列式不等于0的时候，说明矩阵可以有逆矩阵，这里介绍求矩阵的逆矩阵的3种方法。工具/原料more矩阵MATLABmatlab方法1/3分步阅读
2/3
3/3
行变换方法1/1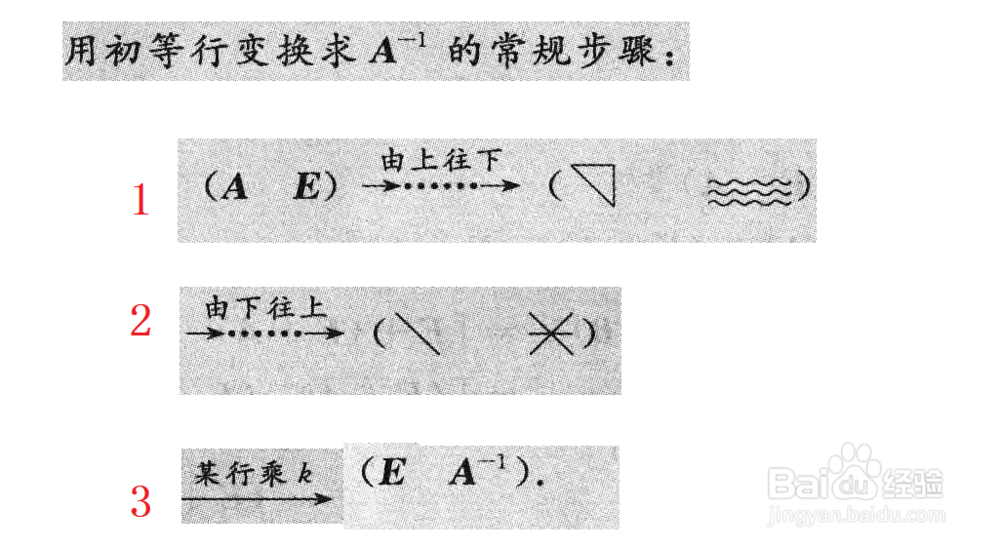
定义法1/2
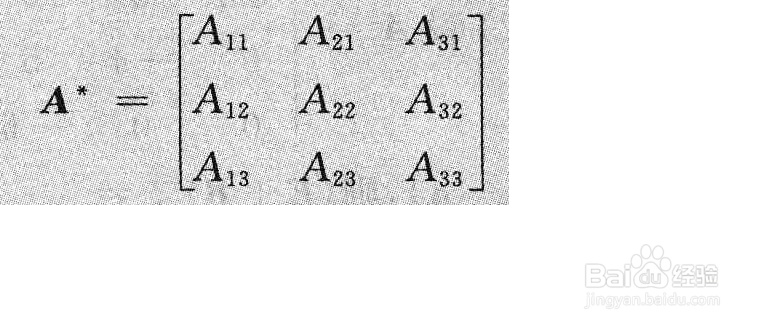2/2
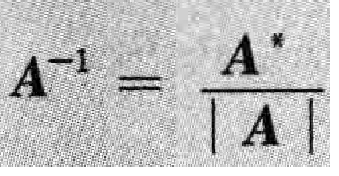注意事项
输入矩阵：
A=
2/3求取矩阵对应行列式的值，det(A)不等于0，逆矩阵才存在。
det(A)
ans =
-7
3/3输入A^-1命令，即可求得逆矩阵。
行变换方法1/1（A,E）经过行变化变为（E,A^-1）
定义法1/2求出A的伴随矩阵A^*。
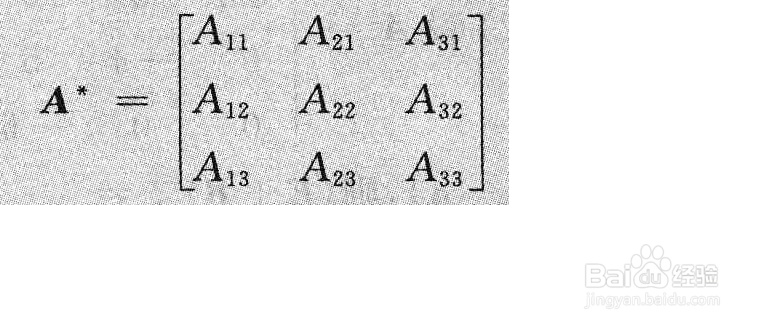2/2利用A^-1=(A^*)/|A|求可逆矩阵。
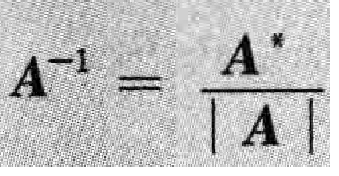注意事项矩阵行列式不为零才是可逆矩阵。
矩阵可逆可逆矩阵版权声明：
1、本文系转载，版权归原作者所有，旨在传递信息，不代表看本站的观点和立场。
2、本站仅提供信息发布平台，不承担相关法律责任。
3、若侵犯您的版权或隐私，请联系本站管理员删除。
4、文章链接：http://www.ff371.cn/art_444836.html
上一篇：简笔画甘蔗怎么画？
下一篇：苦瓜怎么保存到冬天食用
