本经验通过函数的定义域、单调性、凸凹性、极限等性质，介绍函数用导数工具画函数y=5x^3-6x^2的图像的主要步骤。

函数的定义域，根据函数特征，函数自变量可以取全体实数，即定义域为：(-∞，+∞）。

 定义域的定义为：设A，B是两个非空的数集，如果按某个确定的对应关系f，使对于集合A中的任意一个数x，在集合B中都有唯一确定的数f(x)和它对应，那么就称f:A--B为集合A到集合B的一个函数，记作y=f(x)，x属于集合A。

求出函数驻点，由一阶导数的正负，判断函数的单调性，并进一步求解得到函数的单调区间。

函数的单调性也叫函数的增减性。当函数 f(x) 的自变量在其定义区间内增大(或减小)时，函数值f(x)也随着增大(或减小)，则称该函数为在该区间上具有单调性。

通过函数的二阶导数，得函数的拐点，解析函数的凸凹区间。

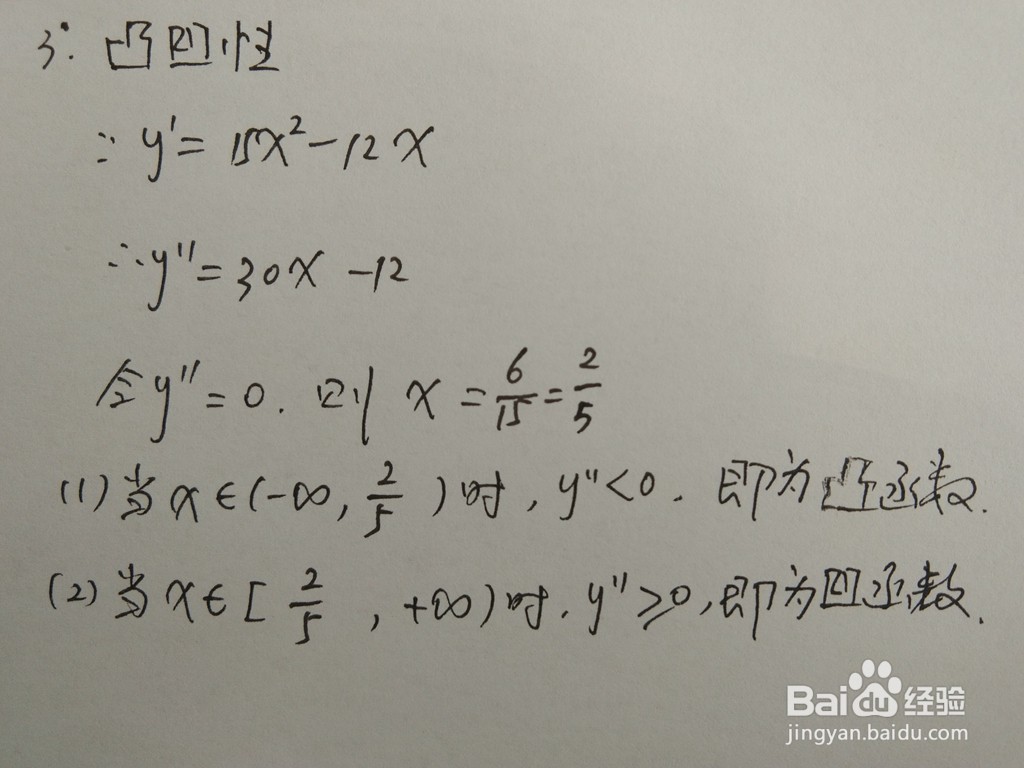
如果函数f(x)在区间I上二阶可导，则f(x)在区间I上是凹函数的充要条件是f''(x)>=0;f(x)在区间I上是凸函数的充要条件是f''(x)<=0。

判断函数在端点处的极限：

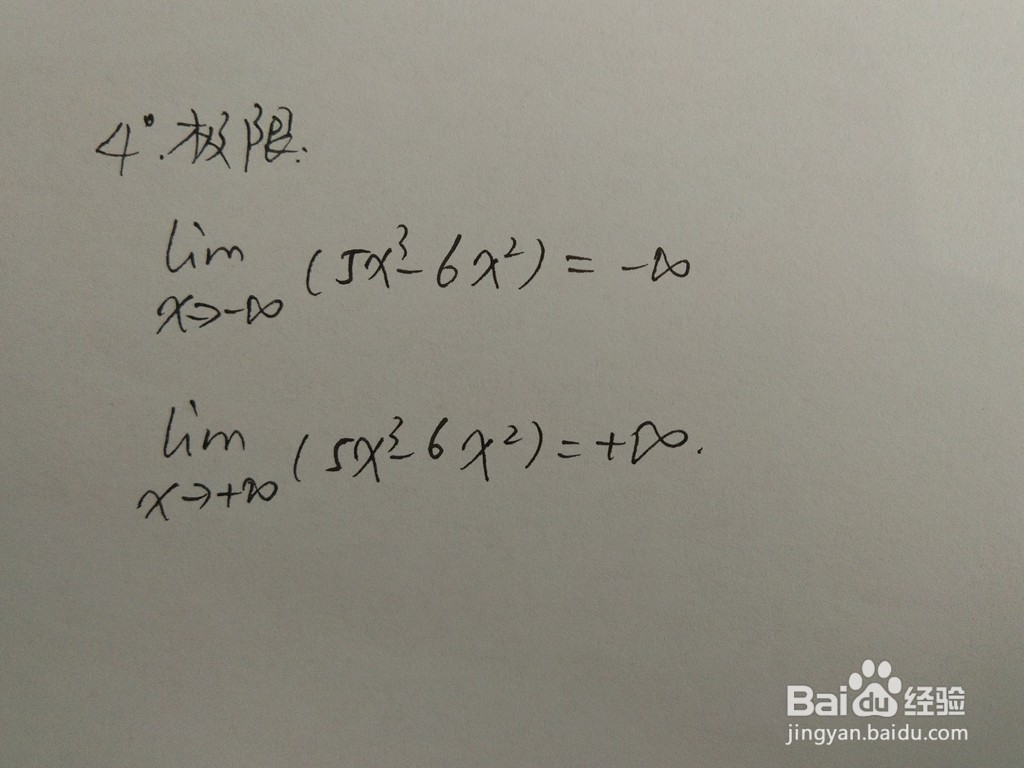
函数部分点，解析函数上部分点如下：

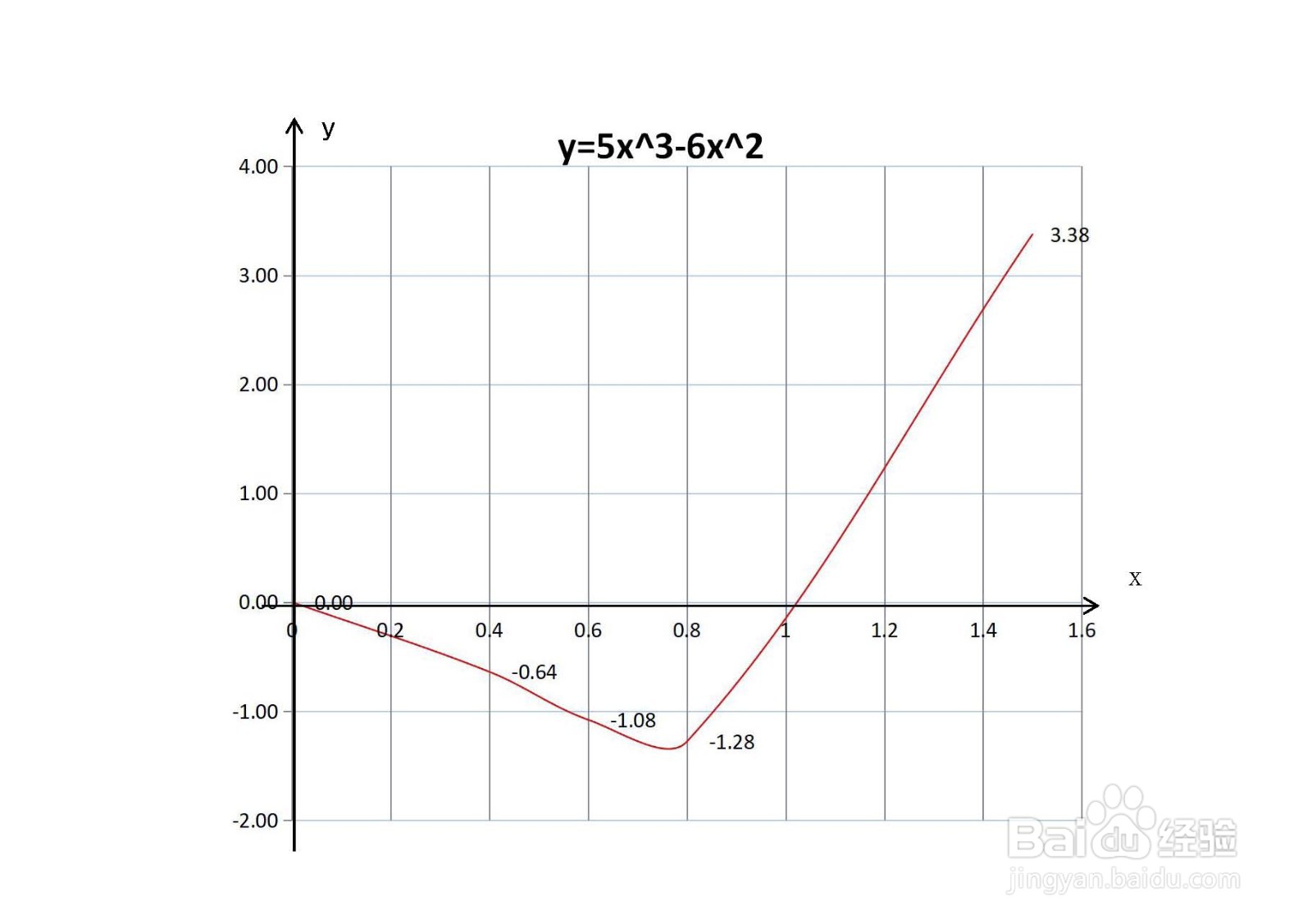
综合以上函数的定义域、值域、单调性、凸凹性和极限等性质，函数的示意图如下：