二叉树的重要性质有哪些
来源:网络收集 点击: 时间:2024-02-13【导读】:
现在有很多朋友都在学习数据结构,其中二叉树是一个很重要的知识章节。二叉树有很多重要性质,它们分别是什么呢?今天就让小编来帮助大家一起来解决这个问题吧!工具/原料more三个二叉树重要性质,两个完全二叉树重要性质性质解释方法/步骤1/5分步阅读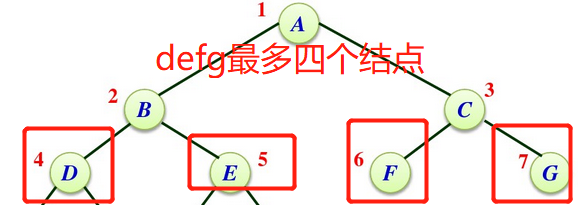 2/5
2/5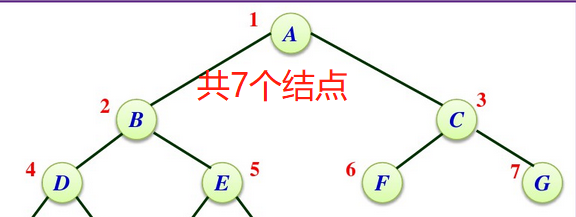 3/5
3/5 4/5
4/5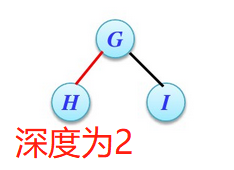 5/5
5/5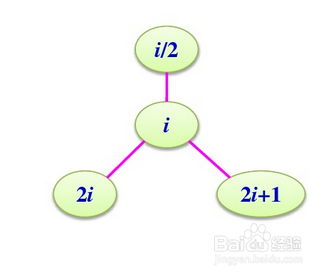 注意事项
注意事项
首先我们要清楚,二叉树有五个重要性质。第一个性质:在二叉树的第i层上至多有2^(i-1)个结点(i≥1)。例如:在如下图所示,在第三层最多只有4个结点,分别是defg。
 2/5
2/5然后是第二个重要的性质:深度为k的二叉树至多有2^(k)-1个结点(k≥1)。如下图所示,深度为3的二叉树最多有一共7个结点,ABCDEFG。
 3/5
3/5第三个重要性质是:对于任何一个二叉树,如果叶子结点为n0个,则度为2的结点的个数为n0-1个,即n0=n2+1。具体的证明过程如下图所示,感兴趣的同学可以看一下,不难推导。
 4/5
4/5以上三个重要性质适用于每一个二叉树,但是接下来的两个性质仅适用于完全二叉树。第一个是,具有n个结点的完全二叉树的深度为+1。比如具有3个结点的完全二叉树的深度为2.
 5/5
5/5最后一个性质:如果对一个有n个结点的完全二叉树的结点按层序编号,有:
① 如果i=1,则结点i是二叉树的根,无双亲;如果i≥1,则其双亲是节点 。
② 如果2i>n,则结点i无左孩子(节点i为叶子节点);否则其左孩子LCHILD(i)是节点2i 。
③ 如果2i+1>n,则结点i无右孩子;否则其右孩子是结点2i+1 。
如下图所示。
 注意事项
注意事项原创不易,禁止转载,违者必究!
喜欢请点赞!
二叉树重要性质数据结构树的重要性质有哪些版权声明:
1、本文系转载,版权归原作者所有,旨在传递信息,不代表看本站的观点和立场。
2、本站仅提供信息发布平台,不承担相关法律责任。
3、若侵犯您的版权或隐私,请联系本站管理员删除。
4、文章链接:http://www.ff371.cn/art_40671.html
上一篇:如何制作有趣的玩具
下一篇:长虹电视遥控器没反应怎么办
 订阅
订阅